堆优化Dijkstra

适用范围

• 最短路径问题->单源最短路->所有边权都是正数
• 稀疏图，即边数$m \le 点数n$
• 用邻接表储存

  时间复杂度

  $mlogn$

  原理解释

• dist表示点离起点的距离，st存储每个点离起点的最短值
• 1.dist[1] = 0; // 表示1到起点距离为0
• 2.遍历所有点，找到不属于st的点中离起点最近的点，记录为t
• 将其存入st中
• 用t这一点更新其他点离起点的距离
• 上述与朴素Dijkstra相同，但进行2时，我们使用优先队列处理,同时存储图 我们使用邻接表处理

例题

https://www.acwing.com/problem/content/852/

AC代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <queue>

using namespace std;

const int N = 1000010;
typedef pair<int, int> PII;

int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c,ne[idx] = h[a], h[a] = idx ++; 
}

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0,1});
    while(heap.size())
    {
        auto t = heap.top();
        heap.pop();
        int distance = t.first, ver = t.second;
        
        if(st[ver]) continue;
        st[ver] = true;
        
        for (int i = h[ver]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(dist[j] > dist[ver] + w[i])
            {
                dist[j] = dist[ver] + w[i];
                heap.push({dist[j], j});
            }
        }
    }
    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}
int main()
{
    memset(h, -1, sizeof h);
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; i ++)
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }
    printf("%d\n", dijkstra());
    return 0;
}

add()解释

e[idx]表示的是a有一条连向b的边，所以e[idx]存的是b.
ne[idx]和h[a]其实是这样的：将a能到的所有点存在
一个连表里，表头就是h[a]，h[a]=idx++就是让从a
的表头指向第idx条边，这样就实现从a这个节点能遍
历到第idx条边.
ne[idx]=h[a]事实上也就是对应链表里的插入操作中
把next指针指向表头所指向的点，让第idx条边能够
遍历到h[a]原来指向的这个点，和h[a]=idx++搭配
后实现遍历a的邻点。

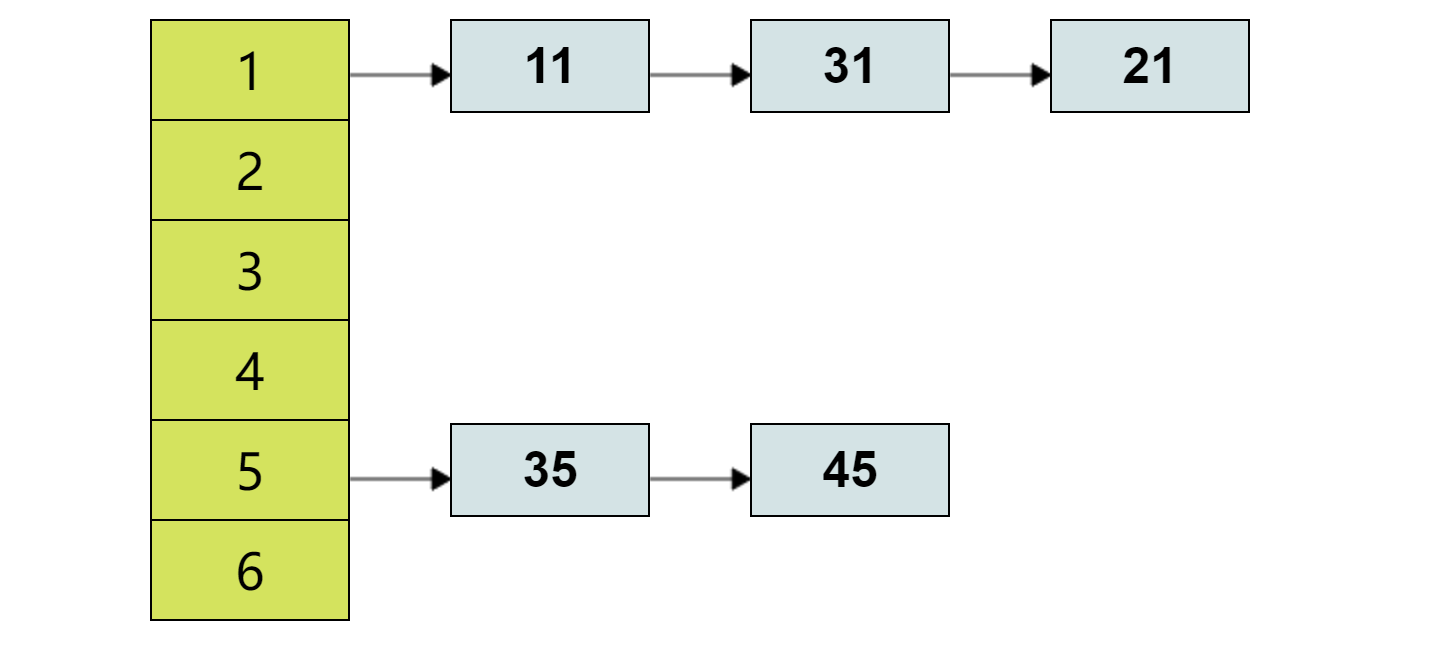
邻接表

我们使用数组模拟链表来储存图

e[idx] = b, w[idx] = c,ne[idx] = h[a], h[a] = idx ++; 

• e[idx] = b,这里用来表示第idx条边指向b
• w[idx] = c,用来存储边权值
• ne[idx] = h[a], 表示第idx条边的是由a为起点的
• h[a] = idx ++,一方面让idx + 1，另一方面使h[a]一直记录为a的最后一条边，以此通过ne[idx] 找到上一个边，直至找完所有与a有关的边，从而实现遍历所有与a有关的边。