二叉树寻路

在一棵无限的二叉树上，每个节点都有两个子节点，树中的节点 逐行 依次按 “之” 字形进行标记。

如下图所示，在奇数行（即，第一行、第三行、第五行……）中，按从左到右的顺序进行标记；

而偶数行（即，第二行、第四行、第六行……）中，按从右到左的顺序进行标记。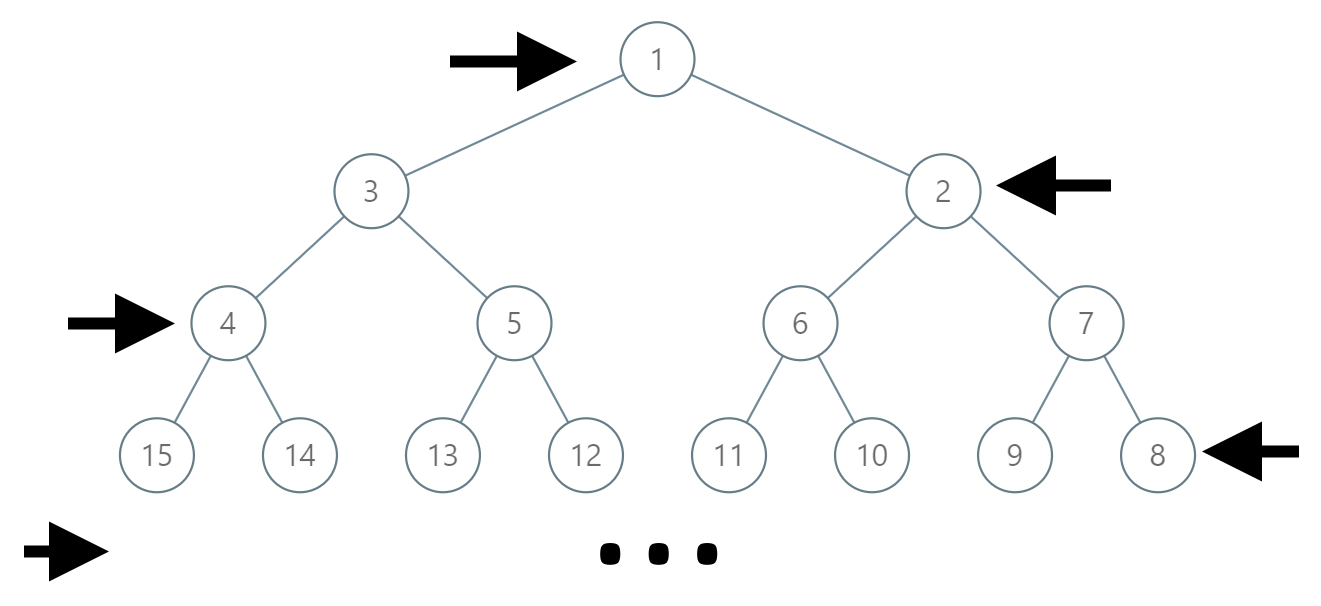

给你树上某一个节点的标号 label，请你返回从根节点到该标号为 label 节点的路径，该路径是由途经的节点标号所组成的。

• 来源：力扣（LeetCode）
• 链接：https://leetcode-cn.com/problems/path-in-zigzag-labelled-binary-tree

  示例

• 输入：label = 14
• 输出：[1,3,4,14]

思路

由于这题是寻找路径，所有我的想法是，先找到目标label结点，根据完全二叉树的特点，逐步找到有关的路径。

1.此题奇数行是正序，偶数行是逆序。
2.且目标结点的一半一定在上一行的结点中。
3.其中目标结点的上一个结点数字label，与上一层结点的中间结点mid有一定关系

• 若mid >= label,路径为：mid + (mid - label) + 1;
• 若 mid < label,路径为：mid - (label - mid) + 1;

4.先前存储路径是由大到小，目标输出是由小到大，最后倒置一下就ok了

AC代码

class Solution {
public:
    vector<int> pathInZigZagTree(int label) {
        stack<int>s;
        vector<int>ret;
        while (label>1) {
            s.push(label);
            label /= 2;        
            if (label == 1) {
                break;
            }
            int h = log2(label) + 1; 
            int mid = (pow(2, h - 1) + pow(2, h) - 1) / 2;  
            if (label <= mid) {             
                label = mid + (mid - label) + 1;
            }
            else {
                label = mid - (label - mid) + 1;
            }
        }
        s.push(1);
        while (!s.empty()) {
            ret.push_back(s.top());
            s.pop();
        }
        return ret;
    }
};