二叉树中第二小的结点

给定一个非空特殊的二叉树，每个结点都是正数，并且每个结点的子结点数量只能为 2 或 0。如果一个结点有两个子结点的话，那么该结点的值等于两个子结点中较小的一个。

更正式地说，root.val = min(root.left.val, root.right.val) 总成立。

给出这样的一个二叉树，你需要输出所有结点中的第二小的值。如果第二小的值不存在的话，输出 -1 。

• 题目来源力扣：https://leetcode-cn.com/problems/second-minimum-node-in-a-binary-tree/

示例一

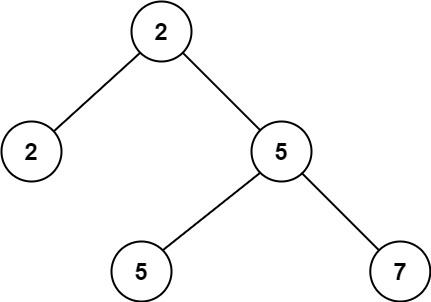
输入：root = [2,2,5,null,null,5,7]
输出：5
解释：最小的值是 2 ，第二小的值是 5 。

示例二

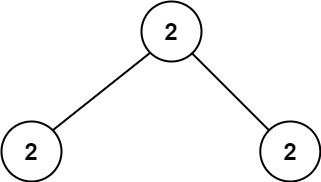
输入：root = [2,2,2]
输出：-1
解释：最小的值是 2, 但是不存在第二小的值。

思路：

根据题目要求，父结点一定是他和两个子结点中最小的，且如果有两个子结点，一定有一个以上的子结点与父结点相等，所以第二小的结点一定在字结点中较大的那个结点所在的路径里。
利用递归遍历结点，很容易写出代码。

AC代码

class Solution {
public:
    int findSecondMinimumValue(TreeNode* root) {
        return firstbigger(root, root -> val);
    }
    int firstbigger(TreeNode* root, int val) {
        if (!root) return -1;
        if (root -> val > val) return root -> val;
        int l = firstbigger(root -> left, val);
        int r = firstbigger(root -> right, val);
        if (l < 0) return r;
        if (r < 0) return l;
        return min(l, r);
    }
};